Historia de las Matemáticas


Con ello se espera que la sociedad entienda porque son importantes las matemáticas y la relación que tienen en la vida diaria.
Introducción
Se dará a conocer como principal objetivo el inicio de los números, la importancia de cómo y con qué fin se crearon los sistemas que cada uno de los diferentes civilizaciones implementaron como lo es la Romana, Egipcia, Babilónica y el sistema binario para poder contar, hacer trueques ,comprar cosas en el mercado, todo ello se creo por medio de las necesidades que la humanidad fue teniendo .
Números Mayas:
- Los mayas fueron una civilización asentada en la parte central del continente americano, concretamente abarcando lo que hoy en día es el sur de México y Guatemala, durante un período comprendido entre el 2.000 a.c. y el 1.697 d.c.
- Sistema de numeración propio, por lo que el origen de los números mayas lo podemos encontrar ante la necesidad de medir el tiempo (días, semanas, años) y no para hacer cálculos matemáticos.
- La civilización maya fue la primera de América e idear el cero , aunque solo con un valor posicional ,además tiene el papel de indicar una ausencia de una cantidad. Los mayas estudiaron de forma precisa los movimientos del sol,la luna y Venus ,también llegaron a la conclusión de que el año solar tenia 365,242 días ,fueron motivados a utilizar números gracias a que tenían varios calendarios.
- Los números mayas podrían ser representados de tres formas diferentes: una mediante formas de cabezas, mediante figuras completas y la que te vamos a presentar a continuación:
Un punto: cuyo valor era 1
Una raya: con valor 5
Un caracol, concha o semilla: de valor 0
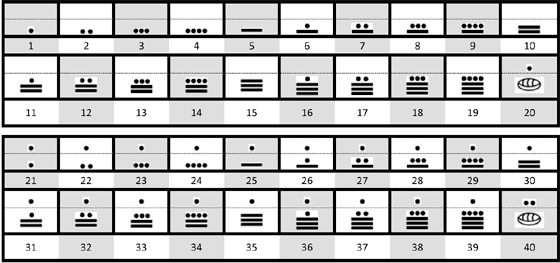
Características del sistema Maya

- Es un sistema vigesimal puesto que agrupa las diversas cantidades de 20 en 20.
- Es un sistema posicional,vertical y ascendente en el que cada piso tiene un valor exponencial diferente.
- Los números mayas fueron los primeros en América que incluyeron el número cero en sus cálculos.
- De número maya a número decimal
- El piso inferior comprende los valores de 0 a 19. El siguiente piso superior representa la cantidad de veintenas que hay, es decir, si en este piso hay un punto, representa el 20; si hay dos puntos representa el 40; si hay una raya y un punto sería 6*20=120.En el caso del tercer piso se hablaría ya de veintenas de veintenas, es decir 20² o grupos de 400 y así sucesivamente con los pisos superiores.
- Números Egipcios
La numeración egipcia, y por ende, los números egipcios fueron un apartado importante dentro de la historia del antiguo reinado faraónico.
Los números egipcios eran representados con diversos ideogramas.

El sistema de numeración egipcio representaba números que abarcaban desde el uno hasta millones, apareciendo en los inicios de la escritura jeroglífica.
Tres milenios antes de la era de Cristo, los egipcios ya contaban con el primer sistema desarrollado de numeración con base 10. Este permitía el uso de grandes números, describiendo también pequeñas cantidades en forma de fracciones unitarias, llamadas las fracciones del Ojo de Horus.
Pero a pesar de este gran desarrollo dentro de la escritura numérica, la misma apenas fue empleada en la vida diaria de los egipcios. Esto se debe a que la mayor parte de los textos administrativos se encontraban escritos en papiro o en ostraca en lugar de tallarse en piedra, y la gran mayoría de los textos que empleaban el sistema numeral egipcio utilizaban la notación hierática.
Según los antiguos griegos,los egipcios dominaban las matemáticas avanzadas,de hecho,a ellos se les atribuye las bases de la actual. Efectivamente,los egipcios utilizaban un sistema de transcripción de números cardinales y ordinales.
- El de números enteros se basaba en un sistema decimal.Por ejemplo,el número 1,se escribía con una simple línea vertical,y para el 9 dibujaban nueve líneas,no tiene ningún misterio.
- Se utilizaba el mismo método para los símbolos del 10,que se escribía por tanto tres veces para referirse al treinta y así sucesivamente para los casos del 100,del 1.000,del 10.000 y del 100.000.
- Por lo visto, y a partir de lo visto en jeroglíficos, los nombres de los números eran: ua (1), senu (2), jemet (3), fedu (4), diu (5), seresu (6),sejef (7), jemenu (8), pesedyu (9), medyu (10), dyebati (20),maba (30), jem (40), diiu (50), seresiu (60), sefejiu (70), jemeniu (80), pesedyiu (90),shet (100), ja (1.000), dyeba (10.000),jefen (100.000) y jej (1.000.000).
- Por otro lado estos nombres casi nunca se escribías y para escribir lass fechas eran muy utilizados los ordinales: tepi era el “primero”,del dos al nueve se añadía la desinencia “nu” al cardinal,así,el tercero era “jemetnu” (jemet+nu).A partir del diez se ponía “mej” delante,de manera que mej-13 era algo como decimotercero.
Otras aportaciones a las matemáticas
Por ejemplo a la construcción de las pirámides, cuyo tamaño, número de bloques y orientación es aún hoy un prodigio de ingeniería y exactitud matemática. Los egipcios podían calcular áreas y superficies, volúmenes y dominaban a la perfección las medidas. También fueron unos de los padres fundadores del álgebra.

Números Romanos
Está considerado como un sistema de numeración no posicional en el cual se emplean ideogramas simples, siete letras mayúsculas que cada una de ellas se corresponde con un valor numérico. La numeración egipcia, los símbolos romanos se escriben y se leen de izquierda a derecha, siempre se encuentran de mayor a menor valor.

Como decimos, los números romanos están formados por una serie de letras. Estas son:
I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1.000
Ejemplo:
¿cómo representar números muy grandes en números romanos? Según este sistema, nunca se podría llegar a 4.000, de hecho el mayor número al que se podría llegar sería MMMCMXCIX (3000 + 900 + 90 + 9 = 3.999.V ¿Cómo podríamos llegar a 4.000?
Muy sencillo, simplemente se añade una línea horizontal encima del número para indicar que ese número se multiplica por mil. Así, para representar el número 4.000 con números romanos se por IV con una línea horizontal por encima.

Números Binarios

Números binarios es: Son números que están dentro del sistema binario de numeración que está constituido por dos cifras 1 y 0, un sistema en el cual se escriben cantidades, códigos, mensajes y otros lenguajes con tan solo dos elementos dentro de la numeración, haciendo que el código se simplifique la comprensión de los sistemas informáticos, pues hará que un elemento tenga un valor unitario o nulo. Es decir que se trabaja en un sistema de puertas cerradas o abiertas. Una ambivalencia. Los elementos que se utilizan son el número uno (1) y el cero (0), donde el 1 significa que la puerta está abierta y el 0, que da como resultado que este elemento sea nulo o que la puerta esté cerrada por lo que la información ignorará este espacio.
Este sistema entonces se basa en posiciones, si la primera posición está abierta tendremos como resultado el número 1. Si tenemos dos posiciones, la primera abierta y la segunda cerrada, tenemos como resultado el número 10. Si tenemos tres posiciones, donde la primera está abierta, la segunda cerrada y la tercera abierta nuevamente, se obtiene como resultado el número 101. Y así sucesivamente, hasta completar el paquete de información que se desea hacer dentro de la representación de los números binarios.
En ocasiones también se pueden encontrar otro tipo de representación como líneas verticales y líneas horizontales para poder representar los dos valores, o quizás una cruz y un círculo del mismo modo que se explicaba las puertas abiertas X y las puertas cerradas O.
Números Binarios Del 1 Al 10
El número uno en decimal es 1, y en binario también es 1.
De la misma manera el 0 de los decimales también es 0 en el binario pues ambos son el principio de la serie, sin embargo a continuación puede haber un poco de confusión en la numeración binaria.
El 2 en decimal es 10 en binario.
El 3 es 11.
El 4 es 100.
El 5 es 101.
El 6 es 110.
El 7 es 111.
El 8 es 1000.
El 9 es 1001
Y el 10 es 1010.
Para Qué Sirven Los Números Binarios
El sistema binario de numeración es utilizado con mucha frecuencia y fue el origen de los sistemas informáticos como las calculadoras y las computadoras. Esto se debe a que la simplificación del lenguaje logra un nivel bajo de error pues se basa en dos únicas respuestas por parte del interprete. Es decir, que solo puede haber dos interpretaciones por cada símbolo. Una puerta está abierta o cerrada, nunca puede haber un valor intermedio. Es como si la respuesta a cualquier pregunta fuera sí o no. 1 o 0. Apagado o encendido. Entonces los transistores y chips de un aparato pueden o no conducir la corriente de información en estos dos únicos sentidos.
Conclusión:
Como se observa en el siguiente trabajo se maneja la importancia de los números desde antes de nuestra era , los diferentes personajes que hicieron posible su descubrimiento , el uso e interés que se tiene por las actividades de la vida cotidiana , gracias a ello existen los intercambios , compra y venta y sobre todo el poder mantener o satisfacer las necesidades.
Bibliografía :
https://numerosbinarios.net/
https://sobrehistoria.com/numeracion-egipcia-y-numeros-egipcios/
https://sobrehistoria.com/numeros-romanos/



